Version Arabe en PDF: اقتران-شهر-شوّال-1439-هجريّ-13-جوان-2018
La conjonction entre la Lune et le Soleil de la fin du mois de Ramadan 1439 H surviendra le 13 juin 2018 à 19h 43mn 13sec TU. Cette conjonction mettra fin à un mois lunaire court de 29,3301829 jours soit plus court que le mois lunaire moyen de 4 heures et 49mn. A l’instant de la conjonction, nous aurons:
- Longitude écliptique moyenne de la Lune: 82° 44′ 43,3″
- Latitude écliptique moyenne de la Lune: -03° 34′ 40,9″
- Parallaxe équatoriale horizontale de la Lune: 1° 00′ 47,3 ″
- Distance géocentrique de la Lune: 360721,0 km
- Vitesse angulaire en longitude de la Lune par rapport aux étoiles:14,98°/j ; par rapport au Soleil: 14,03°/j
Et comme l’inclinaison de l’écliptique sur l’horizon ouest est forte pour les observateurs de l’hémisphère nord, et que la Lune est proche du périgée qu’elle atteindra le 14 juin 2018 à 23h53 TU, l’élongation et la hauteur de la Lune de nuit en nuit croîtront rapidement particulièrement les 3 premiers jours suivant la conjonction.
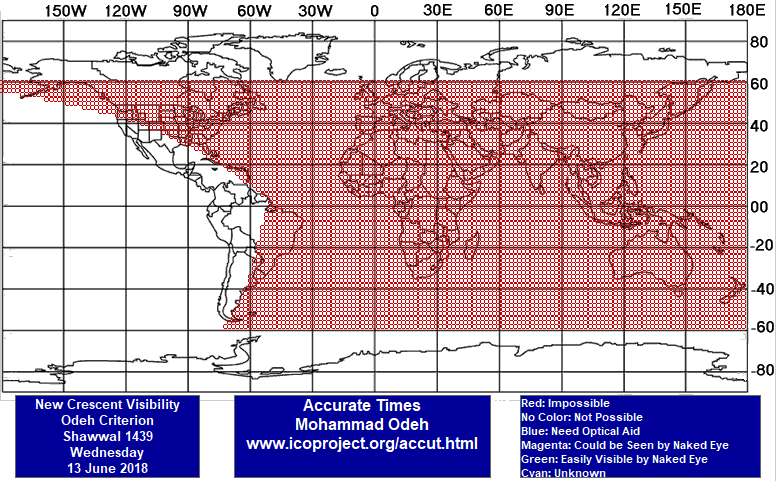
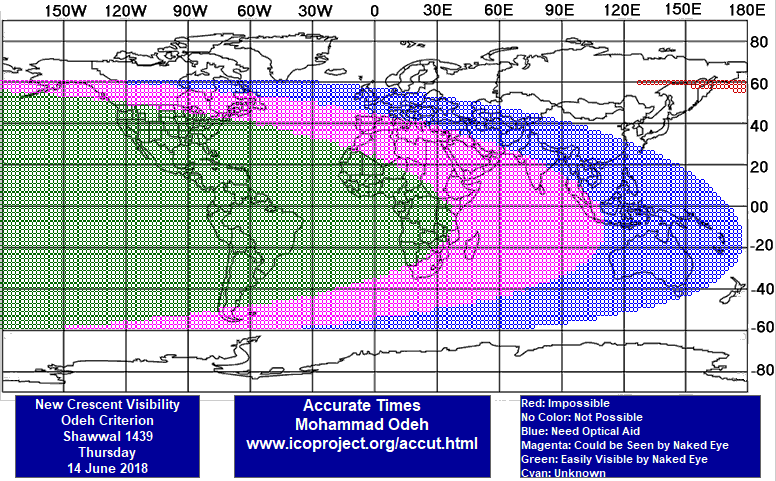
La carte ci dessous, générée par le logiciel ACCURATE TIMES, montre l’aire de visibilité du croissant lunaire selon le critère d’Odeh le 13 juin 2018. Le croissant ne sera alors visible nulle part du monde . L’application du critère turc (critère de Danjon modifié), pour le centre de la Terre (conditions géocentriques), laisse présager une visibilité du croissant lunaire le 14 juin 2018 à partir de 8h 22mn TU, ce qui permettra l’observation du croissant de tous les pays musulmans le soir de ce jour, et ce à partir de l’ouest de l’océan pacifique.
Comme la nuit du doute sera le 14 juin 2018, les circonstances locales n’ont été calculées que pour ce dernier jour.
A Tunis, la Lune se couchera le 14 juin 2018 environ 45 minutes après le Soleil qui se couchera à 18h40 TU (19h40 TL), et la Lune sera à une hauteur de 6,9° et à une élongation de 13° du Soleil, ce qui permettra d’observer la Lune aisément au télescope et délicatement à l’œil nu.
A la Mecque, le 14 juin 2018, la Lune se couchera 44 minutes (19h51 TL) après le Soleil (19h07 TL). A l’instant du coucher de Soleil, a hauteur de la Lune sera de 7,7° et son élongation de 11,4°, rendant aisée son observation au télescope et probablement aussi à l’œil nu.
EN CONCLUSION:
La visibilité du croissant lunaire de Shawal 1439H sera possible des pays arabes et musulmans, le soir du 14 juin 2018, laissant présager que le commencement de Shawal serait annoncé le soir même après le coucher du Soleil, et comme premier jour de l’aîd le 15 juin 2018.
Faites un geste noble et soutenez la science
C’est en donnant que tu recevras.